Оценка стойкости грунтов к разжижению по данным шведских весовых испытаний

Коррозионная стойкость грунта

Предложена методика оценки сопротивления грунтов разжижению с помощью шведского весового зондирования. Эмпирические формулы, оценивающие сопротивление разжижению грунтов R l непосредственно из сопротивления проникновению W sw и N sw , полученных при шведском весовом зондировании, сначала получают путем объединения корреляции между значениями W sw и N sw и относительной плотностью D r и связь между сопротивлением разжижению R l и относительной плотностью D rполученные в прошлых исследованиях.

В результате выводятся две эмпирические формулы, одна для песка, а другая для песка с илом и пылеватого песка. Затем предложенная процедура сравнивается с традиционной процедурой и подробно изучается. Установлено, что предложенная методика хорошо работает для песка, песка с илом и илистого песка, хотя при ее применении к мелким илам следует проявлять должную осторожность.

Вступление

После Великого восточно-японского землетрясения 2011 г., которое произошло на востоке материковой части Японского архипелага 11 марта 2011 г., многочисленные жилые дома были повреждены из-за осадки и наклона, вызванных разжижением почвы .

Дома располагались в основном на мелиорированных землях вдоль Токийского залива. Некоторые последние разработки были сделаны в области геотехнических исследований.инструменты для оценки склонности почв к разжижению в Японии, в том числе конус с пьезоэлектрическим приводом (PDC). Тем не менее, шведские весовые зондирования (SWS) широко использовались и будут по-прежнему использоваться в Японии для геотехнических исследований жилых домов в качестве надежного и экономичного инструмента. Кроме того, тесты SWS являются инструментами расследования, официально рекомендованными для этой цели Министерством земли, инфраструктуры и транспорта Японии.

Следовательно, очень важно продолжать более продвинутое использование тестов SWS. Процедура тестов SWS и интерпретация результатов тестов описаны Tsukamoto et al. (2004) . Процедура испытания состоит из двух этапов: статического проникновения и вращательного проникновения. Во время фазы статического проникновения винтообразное острие, прикрепленное к наконечнику стержня весом 49 Н (5 кг f), статически пробивается путем постепенного добавления нескольких грузов (10, 10, 25, 25 и 25 кг f). до тех пор, пока общая нагрузка не станет равной 980 Н (100 кгс ), как показано на рис. 1 .

При каждом приращении нагрузки измеряется глубина статического проникновения, а общий вес обозначается как W sw(кН). При отсутствии статической проходки производят вращательную проходку. Горизонтальная ручка, прикрепленная к вершине стержня, вращается, и число полуоборотов, необходимое для проникновения стержня на 25 см, обозначается как N a . Затем значения N a умножаются на 4 и преобразуются в число полуоборотов на метр, N sw (ht/m).

Непосредственно измерить глубину залегания грунтовых вод по испытаниям ЗС невозможно, хотя оценить глубину, наблюдая границу между сухой и мокрой поверхностями стержня во время его извлечения, все же возможно. Кроме того, также невозможно классифицировать типы грунтов и почвенных слоев по тестам SWS. Хотя некоторые новыеОборудование для отбора проб почвы было разработано недавно, его пригодность еще предстоит проверить.

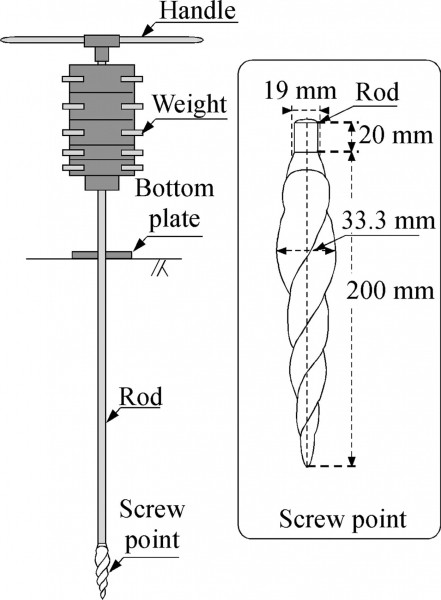
Рис. 1 . Шведское испытательное оборудование для измерения веса.

Использование испытаний SWS было тщательно изучено для оценки инженерных свойств грунтов и различных параметров, связанных с разжижением грунта , таких как относительная плотность, значение SPT N , прочность на сдвиг в недренированном состоянии, коэффициент безопасности против разжижения, пост-ожижение . оседание и боковое смещение ( Tsukamoto et al., 2004 , Tsukamoto et al., 2009a , Tsukamoto, 2009b , Tsukamoto et al., 2009c , Tsukamoto and Ishihara, 2011 , Tsukamoto et al., 2012 , Tsukamoto et 13, 20 , Цукамото, 2015 г.; Цукамото и Исихара, 2011 г. ).

Однако для оценки сопротивления разжижению в этих предыдущих исследованиях требовались некоторые свойства почвы, такие как диапазон коэффициента пустотности e max – e min и средний диаметр частиц D 50 . Кроме того, необходимо было пройти сложную последовательную процедуру, включающую преобразование значений W sw и N sw в значения SPT N с последующим преобразованием SPT N- значения сопротивления разжижению. В настоящем исследовании предлагается более надежная процедура для оценки сопротивления грунтов разжижению с помощью испытаний SWS.

2 . Вывод предлагаемой процедуры

Известно , что сопротивление пробиванию N sw при испытаниях SWS в наибольшей степени зависит от эффективного всестороннего напряжения, градации грунта, плотности грунта и т. д. Результаты испытаний лабораторной калибровочной камеры при испытаниях SWS показаны на рис. 2 ( Tsukamoto et al. , 2004 , Цукамото и др., 2009а ). Здесь значения N’ sw1 определяются с учетом эффектов статического проникновения и эффективного ограничивающего напряжения следующим образом:

(1) N s w 1 ′ = ( N s w + 40 × W s w ) 98 σ v ′ = N s w ′ 98 σ v ′

R l = β t x ( D r − D r o ) де W sw в кН инаходится в кПа. В фазе статического проникновения она уступает N’ sw = 40 × W sw [кН], поскольку N sw = 0. С другой стороны, в фазе проникновения с вращением она уступает N′ sw = N sw +40, поскольку W sw =1 [кН]. Это было продемонстрировано Tsukamoto et al. (2009a, 2009b) и Tsukamoto (2009) , что линейная зависимость N′ sw1 = α sw D r 2справедливо для мелкого чистого песка, хотя отношения для песка с илом и илистым песком более подходящим образом можно представить с помощью смещения относительной плотности, D ro , следующим образом:

(2) N s w 1 ′ = α s w ( D r − D r o ) 2

где D r и D ro принимают значения в диапазоне от 0 до 1 и не являются процентами. Значение α sw изменяется при включении ила. Данные, представленные на рис. 2 , ясно показывают сильную зависимость значений N’ sw1 от сортности почвы, которая представлена ​​значением α sw . На основании данных, представленных на фиг.2 , установлено, что смещение равно D ro =25%.

Значения α sw , полученные из рис. 2 , сведены в табл. 1 .. Наличие отклонения в относительной плотности исключительно для песка с илом и илистым песком может указывать на то, что может существовать диапазон коэффициентов пустотности, которого сжимаемый содержащий ил песок не сможет достичь при наличии ограничивающего напряжения.

Рис. 2 . Отношения на графиках для N ‘ sw1 от относительной плотности D r (по Tsukamoto et al., 2009a, 2009b; Tsukamoto 2009 ).
Таблица 1 . Физические свойства почв и предполагаемые параметры в лабораторных испытаниях в калибровочной камере

Пустая ячейка	Д 50 (мм)	Fc ( %)	е макс — е мин	α ув	Дро ( %)
Тойура песок	0.17	0	0.366	690	0
Инаге песок	0.15	23.8	0.512	890	25
Омигава песок	0.15	10.7	0.611	470	25
Нарита песок	0.13	29.1	0.765	235	25

На рис. 3данные по сопротивлению разжижению , R l = σ d,l /(2 σ ′ o ), собранные из многих источников прошлых исследований, нанесены на график в зависимости от относительной плотности D r . Здесь данные, представленные на рис. 3 , представляют собой сопротивление разжижению R l , полученное из изотропно консолидированных недренированных циклических трехосных испытаний на насыщенных образцах грунта, σ ′ o , эффективное всестороннее напряжение, и σ d,l , единичная амплитудациклическое напряжение , используемое для достижения удвоенной амплитуды осевой деформации DAε a =5% за 20 циклов.

Таким образом, любые другие эффекты, включая магнитуду землетрясения, разнонаправленное сотрясение и всестороннее напряжение, выходят за рамки настоящего исследования. Эти данные включают восстановленные образцы, а также ненарушенные образцы и варьируются от песка до ила. Хорошо известно, что сопротивление разжижению увеличивается почти линейно с относительной плотностью вплоть до D r =80%. Однако сопротивление имеет тенденцию к быстрому увеличению, когда относительная плотность превышает D r =80% .).

Сосредоточив внимание на диапазоне данных до D r =80%, показанном на рис. 3 (a), эмпирическое соотношение R l =0,42× D r можно было бы правильно принять для чистого песка . С другой стороны, было бы все еще спорно описывать тенденцию сопротивления разжижению путем изменения включения ила . другие). С точки зрения лучшей характеристики грунтов, состоящих из песчано-пылевых смесей, использование обычных определений пористости и относительной плотности может оказаться неадекватным, и недавно были введены и исследованы понятие пустотности скелета и подобные понятия.

Однако применимость таких концепций к характеристике сопротивления разжижению смесей песка и ила требует более подробного изучения. Тем не менее, хотя данные, представленные на рис. 3 (б), весьма ограничены, они ясно указывают на то, что отношения сопротивления разжижению к относительной плотности,R l / D r будет иметь тенденцию к уменьшению с увеличением количества ила.

Следуя линейной зависимости R l =0,42× D r для чистого песка с относительной плотностью до D r =80%, как описано выше, аналогичным образом было бы целесообразно принять линейные зависимости для пылесодержащего песка с относительной плотностью до D г =80%. Кроме того, стоит посмотреть, не вписывается ли наличие смещения относительной плотности в соотношения между R l и D r , как показано на рис. 3.(б). Видно, что для песка с илом, пылеватого песка и ила можно принять следующие соотношения.

рл=бтИкс(Др−Дрo) R l = β t x ( D r − D r o )
где значение β tx снова меняется при включении ила. Подобно сильной зависимости сопротивления проникновению SWS-испытаний от класса грунта, показанной на рис. 2 , сопротивление разжижению также демонстрирует четкую зависимость от класса грунта, как показано на рис. 3 , что представлено значением для β tx . При построении более надежной эмпирической зависимости между стойкостью к разжижению и стойкостью к проникновению в испытаниях SWS на самом деле основной вопрос заключается в том, будут ли эти два эффекта компрометировать друг друга, как описано ниже.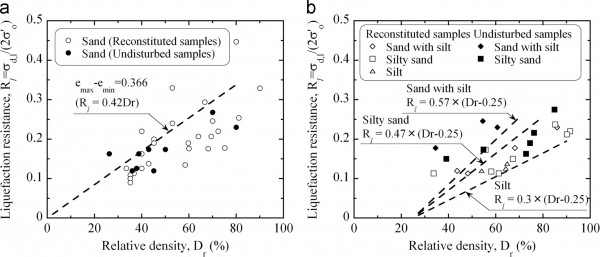

Рис. 3 . Отношения на графиках для R l к относительной плотности D r , (a) песок и (b) песок с илом, илистым песком и илом (данные, собранные Nakazawa 2007 ).

Параметры α sw и β tx в уравнениях (2) , (3) , введены, чтобы принять во внимание эффекты сортировки почвы. Есть некоторые полезные свойства почвы, которые подходят для классификации эффектов сортировки почвы, такие как содержание мелких частиц F c и средний диаметр частиц D 50 . Диапазон коэффициента пустотности, e max – e min , также является одним из свойств почвы, которое может отражать влияние сортировки почвы.

Это было предложено Кубриновски и Исихара (2004) и было показано, что оно прекрасно работает для анализа сопротивления проникновению в ходе испытаний на месте (Кубриновски и Исихара, 1999 г., Цукамото и др., 2004 г. ). Здесь на основании данных, представленных на рис. 2 , отношения N’ sw1 / D r 2 для чистого песка и N’ sw1 /( D r -0,25) 2 для песка с илом и пылеватым песком построены в зависимости от диапазона в коэффициент пустотности, e max – e min , на рис. 4 . Затем данные для песка с илом и илистого песка аппроксимируются следующим уравнением:

N s w 1 ′ ( D r − 0.25 ) 2 = 96 ( e max − e min ) 3.2

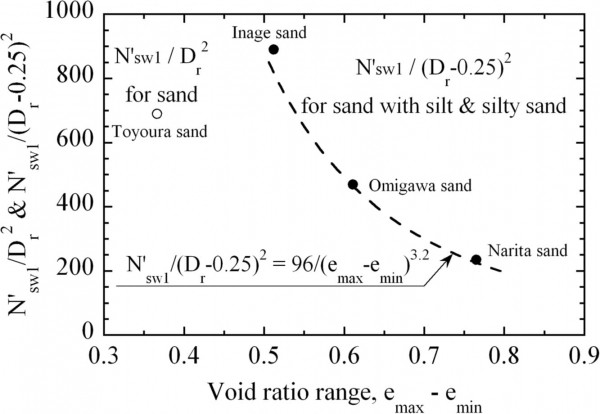
Рис. 4 . Графики данных для N’ sw1 / D r 2 для песка и N’ sw1 / ( D r -0,25) 2 для песка с илом и илистым песком в зависимости от диапазона коэффициента пустотности , e max — e min .

С учетом того же принципа отношения R l / D r для чистого песка и R l /( D r -0,25) для песка с илом и пылеватым песком, показанные на рис. 3 , нанесены в зависимости от диапазона коэффициента пустотности . , e max – e min , показанные на рис. 5 . Затем данные для песка с илом и илистого песка аппроксимируются следующим уравнением:

(5)
R l D r − 0.25 = 0.2 ( e max − e min ) 1.6

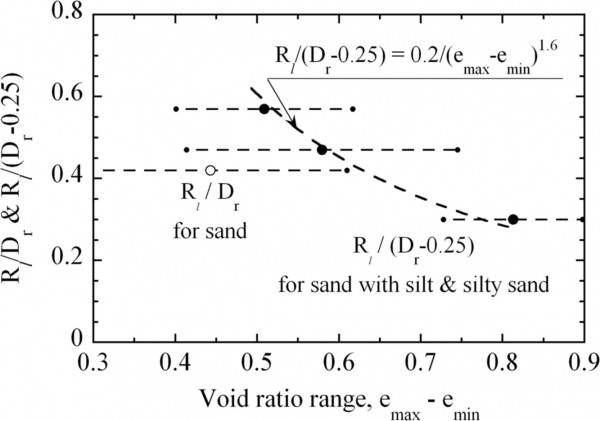
Рис. 5 . Графики данных для R l / D r для песка и R l /( D r -0,25) или песка с илом и илистым песком в зависимости от диапазона коэффициента пустотности , e max – e min .

На основании данных и эмпирических уравнений, представленных на рис. 4 , рис. 5 , корреляции между R l и N’ sw1 могут быть получены для чистого песка и для песка с илом и илистого песка следующим образом:

(6)

R l = 0.016 N ′ s w 1 ( for ​ clean sand of R l ≤ 0.3 )

(7)

R l = 0.02 N ′ s w 1 ( for sand with silt and silty sand of R l ≤ 0.3 )

 

Следует отметить, что параметр почвы e max – e min , представляющий влияние сортировки почвы, был удален и больше не присутствует в уравнениях. (6) , (7) , хотя два эмпирических уравнения были получены как уравнения. (6) , (7) для чистого песка и для песка с илом и илистым песком соответственно. Здесь следует отметить, что уравнение Уравнение (4) разработано для пылеватого песка с содержанием взвешенных частиц F c менее 30 %. Кроме того, на основании графиков корреляции данных F c и e max – e min , полученныхКубриновски и Ишихара (2004) , существует сильная тенденция к увеличению e max – e min с F c до F c =30% (соответствует e max – e min =0,7), выше которой изменение e max – e min с ростом F c становится меньше.

Таким образом, при внимательном рассмотрении данных, показанных на рис. 5 , можно предположить, что использование уравнения. (5) требует некоторой осторожности и должен быть ограничен пылеватым песком с содержанием мелких частиц менее F c=30%. В конце концов, использование уравнения. (7) должны быть ограничены песком с илом и илистым песком.

3 . Проверка предложенной процедуры

Наиболее надежной схемой проверки предлагаемой процедуры является проведение сравнений с наблюдаемым поведением поля. Это требует подтверждения того, действительно ли произошло разжижение грунта , а также надежной оценки амплитуды циклического напряжения сдвига в конкретном месте во время конкретного землетрясения. Это полностью выходит за рамки возможностей авторов; и, таким образом, предлагаемая процедура вместо этого проверяется путем сравнения с обычной процедурой, используемой авторами.

В традиционной процедуре оценка сопротивления разжижению грунтов полностью основывалась на значениях SPT N , как показано на рис. 6 . Следовательно, чтобы использовать испытания SWS, сопротивление проникновению испытаний SWS, W sw и N sw , сначала преобразуется в значенияSPT N. Наиболее часто используютсяэмпирические формулы, предложенные Inada (1960) , хотя Tsukamoto et al. также предложили следующую эмпирическую формулу. (2004) и используется в настоящем исследовании:

(8)

N = e max − e min 10 ( N s w + 40 × W s w )

 

 

 

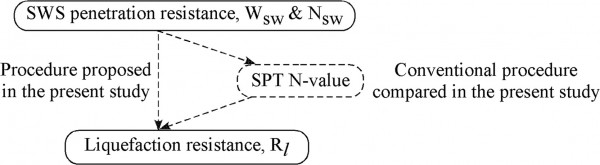
Рис. 6 . Методика оценки сопротивления разжижению грунтов по сравнению с общепринятой методикой.

Использование уравнения (8) выгодно для учета эффектов сортировки почвы способом, относящимся к настоящему исследованию. Из этого следует, что сопротивление разжижению грунтов будет оцениваться по значениям SPT N на основе эмпирических формул, таких как предложенные Tatsuoka et al. (1980) следующим образом:

(9)

где Δ R l ( D 50 )=0,225×log 10 (0,35/ D 50 ), а D 50 выражен в мм. Было отмечено, что уравнение. (9) справедливо для грунтов с D 50 от 0,04 до 0,6  мм. Нецелесообразно или удобно использовать два параметра, а именно e max – e min в уравнении. (8) и D 50 в уравнении. (9) . Здесь значения e max – e min можно преобразовать в D 50приняв соотношение e max – e min =0,23+0,06/ D 50 , предложенное Кубриновским. Эмпирическая формула уравнения. (9) — одно из самых полезных уравнений; он удовлетворительно включает в себя эффекты сортировки почвы. Однако, когда дело доходит до использования тестов SWS без отбора проб почвы , использование уравнений. (6) , (7) предпочтительнее из-за их нечувствительности к сортировке почвы.

Чтобы проверить процедуру, предложенную в настоящем исследовании, проводится сравнение с обычной процедурой с использованием некоторых исследований истории болезни . Исследование истории болезни в Итако-Сити было недавно представлено, и другие исследования истории болезни, описанные в предыдущих исследованиях, используются в дальнейшем.

3.1 . Изучение истории болезни в городе Итако

Город Итако расположен в нижнем течении реки Тоне, как показано на рис. 7 , и является одним из районов, где наблюдалось обширное разжижение почвы во время главного толчка и повторных толчков Великого восточно-японского землетрясения 2011 года ( Tsukamoto et al. , 2012 ). После значительного ущерба инфраструктуре, а также жилым домам, нанесенным из-за разжижения почвы, город Итако инициировал полевые геотехнические исследования , в ходе которых на нескольких участках было проведено исследование траншей. Часть результатов геотехнических исследований описана Tsukamoto et al. (2015) .

Две траншеи, обозначенные здесь как A и B, расположены относительно недалеко от станции JR Итако. История землепользования, безусловно, влияет на слоистость почвенных отложений. В этой области в течение длительного периода времени преобладали рисовые поля , в которых образовались сети небольших водных каналов для сельскохозяйственных целей, таких как орошение и транспорт. Затем этот район был рекультивирован, на нем были построены жилые дома и объекты инфраструктуры. Фактически, одной из основных целей исследования траншей было выяснить, не были ли какие-либо почвенные материалы, рекультивированные в таких старых небольших водных каналах, причиной обширного разжижения почвы, наблюдаемого вокруг этой области.

В траншее А были обнаружены некоторые остатки старых водных каналов, как показано на рис. 8.. Выяснилось, что эти старые водотоки рекультивированы с глинистыми грунтами, по крайней мере, в этом районе, и в меньшей степени ответственны за разжижение грунта. Вместо этого некоторые следы разжижения почвы наблюдались в нижележащем слое мелкого песка, который представляет собой естественное отложение серого цвета, как показано на рис. 8 . Тщательный осмотр траншеи B показал, что питающие дайки для песчаных бурь были очень тонкими, как показано красными стрелками на рис. 9 , и образовались из нижележащих природных песчаных отложений.

Образцы природных песчаных отложений, которые были разжижены, были извлечены из траншей, и распределение размеров зерен показано на рис. 10 . Некоторые физические свойства, относящиеся к данному исследованию, также показаны в таблице 2 .. В двух точках рядом с траншеей А, Sws-1 и Sws-2, и в двух точках рядом с траншеей B, Sws-3 и Sws-4 была проведена серия шведских весовых зондирований.

 

 

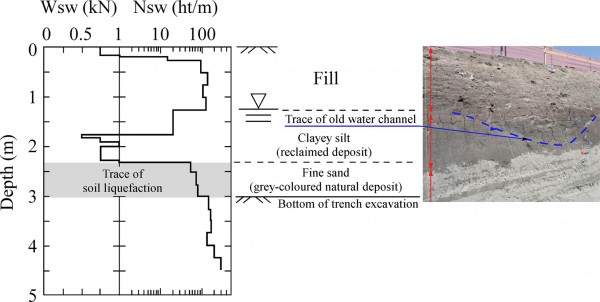
Рис. 8 . Распределение W sw и N sw по глубине и профилям почвы, наблюдаемое в поперечном сечении траншеи на Sw-1 (траншея A в городе Итако).

 

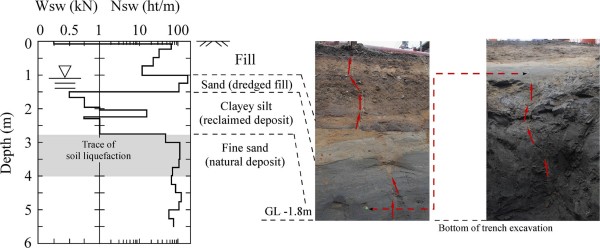
Рис. 9 . Распределение W sw и N sw по глубине и профилям почвы, наблюдаемое в поперечном сечении траншеи на Sw-4 (траншея B в городе Итако). (Для интерпретации ссылок на цвет в легенде к этому рисунку читатель отсылается к веб-версии этой статьи.)

 

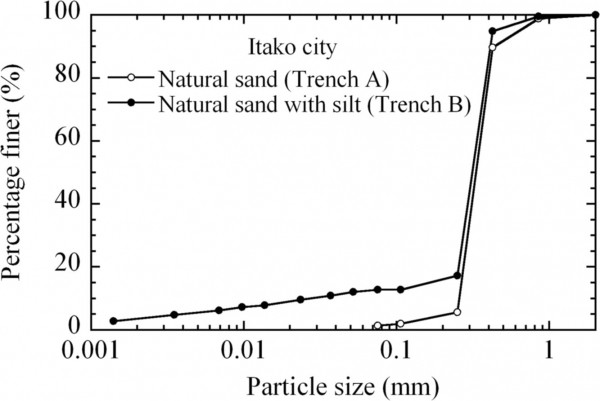
Рис. 10 . Гранулометрический состав почвы, разжиженной во время Великого восточно-японского землетрясения 2011 г. (траншеи A и B в городе Итако).

Таблица 2 . Физические свойства грунтов в исторических исследованиях.

Сайт Д 50 (мм) Fc ( %) е макс е мин Образец почвы уравнение установлен Справка

Желоб А, Италия 0.33 1.4 1.11 0.72 Образец траншеи уравнение (6) Цукамото и др. (2015)

Желоб Б, Италия0.3112.71.580.94Образец траншеиуравнение (7)

Река Тонегава, город Катори 0.13 19.6 1.34 0.82 Образец кипячения песка уравнение (7) Цукамото и др. (2012)

Река Юккен-гава, город Катори 0.14 22.5 1.74 1.01 Образец кипячения песка уравнение (7) Цукамото и др. (2012)

Накаминато, город Хитатинака 0.21 16.0 0.926 0.532 Образец кипячения песка уравнение (7) Цукамото и др. (2013)

Промышленный комплекс Такэноути, город Сакаи-минато 0.045 98 1.586 0.858 Образец кипячения песка уравнение (7) Цукамото и Исихара, 2010 г. , Цукамото и Исихара, 2011 г.

Региональный центр очистки сточных вод Кашивазаки 0.30 12.6 1.057 0.626 Образец кипячения песка уравнение (7) Цукамото и Исихара (2010)

город Карацу 0.40 6.0 – – образец КПТ уравнение (6) Хашимото и др. (2015)

Используя данные W sw и N sw , соответствующие слоям грунта, подвергшимся разжижению, значения сопротивления разжижению R l рассчитывают по предложенной методике по уравнению. (6) или (7) в зависимости от значений содержания мелочи F c . Здесь, когда значение F c ниже примерно 5%, почва классифицируется как песок и уравнение (6) используется. С другой стороны, когда значение F c находится в диапазоне примерно 5–15%, почва классифицируется как песок с илом и уравнением. (7)используется. Когда значение F c превышает примерно 15%, почва классифицируется как илистый песок и уравнение (7) используется.

Значения сопротивления разжижению R l также рассчитываются по обычной процедуре с использованием уравнений (8) , (9) ; они нанесены относительно относительной плотности D r на фиг.11 . Белые точки обозначают данные предлагаемой процедуры, а темные точки указывают данные обычной процедуры. Значения относительной плотности D r рассчитывают по следующей эмпирической формуле, предложенной Tsukamoto et al. (2004) :

(10)

где значения e max – e min также можно оценить по корреляции e max – e min =0,23+0,06/ D 50 , предложенной Кубриновски и Ишихара (2004) . Установлено, что предложенная процедура дает немного более низкие оценки для R l , чем обычная процедура для данных Sws-1 и Sws-2 вблизи траншеи A. С другой стороны, предложенная процедура дает несколько более высокие оценки для R l чем традиционная процедура для данных Sws-3 и Sws-4 вблизи траншеи B. Прямое сравнение данных для R l, рассчитанный по предложенной методике и обычной методике, показан на рис. 12 . На этом рисунке данные линейно аппроксимированы пунктирными линиями.

3.2 . Другие исследования истории болезни из прошлых полевых исследований

Авторы продолжают использовать тесты SWS для разведывательных исследований землетрясений, а некоторые из прошлых полевых исследований используются в качестве тематических исследований в настоящем исследовании, как показано в Таблице 2 . В этой таблице также показаны некоторые свойства почвы, относящиеся к данному исследованию, и типы образцов почвы.

Участки рекультивированных месторождений в городах Итако , Катори и Хитачинака подверглись разжижению почвы во время Великого восточно- японского землетрясения 2011 года . Участок рекультивированных отложений в городе Сакаи — минато подвергся разжижению почвы во время землетрясения Тоттори-кен Сейбу в 2000 году . Образец почвы, извлеченный из этого исследования истории болезни, содержал ил до F c =98%; и, таким образом, использование уравнения. (7)не актуально. Тем не менее, это исследование истории болезни также включено в целях сравнения.

На участке регионального центра очистки сточных вод Кашивазаки произошло разжижение почвы во время землетрясения Ниигата-кен Чуэцу-оки в 2007 году (Tsukamoto and Ishihara, 2010 , Tsukamoto and Ishihara, 2011 ). Месторождение аллювиального песка в городе Карацу в префектуре Сага на Кюсю не подвергалось разжижению почвы во время недавних землетрясений. Тем не менее, были проведены некоторые полевые испытания ультрамикродисперсного цементного раствора с проницаемостью вместе с испытаниями SWS ( Hashimoto et al., 2015 ).

На рис. 13 , рис. 14 показаны сравнения значений R l , рассчитанных по предложенной и обычной процедурам, для участков в городах Катори и Хитачинака. На этих диаграммах и последующих диаграммах пунктирными линиями показаны самые высокие и самые низкие отношения Rl , рассчитанные по предлагаемой методике, к отношениям по обычной методике. Предложенная методика дает более низкие оценки для Rl , чем обычная методика для участков в городе Катори, показанная на рис . 13 , где содержание мелких частиц F cсоставляет около 20%. С другой стороны, предлагаемая методика, по-видимому, дает разумные оценки для R l , аналогичные обычной процедуре для участков в городе Хитачинака, показанной на рис. 14 , где содержание мелких частиц F c составляет 16%. Ниже будут даны некоторые рассуждения о различиях в оценках.

На фиг.15 значения R l , рассчитанные по предлагаемой и обычной процедурам, нанесены в виде зависимости от D r . для территории промышленного комплекса Такэноути в городе Сакаи-минато. Этот участок соответствует рекультивированным отложениям донных отложений , содержащих до 98 % ила . Данные по сопротивлению разжижению, R l = σ d,l /(2 σ ′ o ), также представлены на рис. 15 . Они были получены из насыщенных изотропно консолидированных недренированных циклических трехосных испытаний.проводили на восстановленных образцах ( Imamura et al., 2004 ) и на ненарушенных образцах ( Nakazawa et al., 2004 ). Некоторые из более ранних исследований показали, что сопротивление разжижению ненарушенных образцов илистого песка и ила выше, чем у образцов, восстановленных в лаборатории ( Huang and Huang 2007 , и др.).

Однако данные по сопротивлению разжижению ненарушенных образцов, показанные на рис. 15 , оказались даже ниже, чем по предложенной методике. Некоторые рассуждения о расхождениях в оценках будут даны позже. Сравнение значений R l , рассчитанных по предложенной и обычной процедурам, показано на фиг.16 .

3.3 . Некоторые последствия и ограничения предлагаемой процедуры

На основании сравнений R l , рассчитанных по предложенной и общепринятой методикам и показанных на рис. 12 , 13 , 14 , 15 , 16 , 17 , 18 , диапазоны в отношения для R l , рассчитанные по предлагаемой методике, к отношениям по обычной методике могут быть выведены. На фиг.19 значения для Rl (предлагаемый)/ Rl ( обычный ) затем нанесены на график в зависимости от содержания мелких частиц Fc . Значения R l(предлагаемый)/ R l (обычный) остаются около 1, вплоть до содержания мелочи F c =15%, хотя они имеют тенденцию к уменьшению с увеличением содержания мелочи F c выше F c =15%.

По данным, представленным на рис . 12 , рис. 13 , рис. 14 , рис. 15 , рис. 16 , рис. 17 , рис. процедуры путем расчета значений R l (традиционный)- R l (предлагаемый). На фиг.20 значения R l (обычный) — R l (предлагаемый) нанесены в зависимости от среднего диаметра частиц D 50 . Обнаружено, что большие расхождения возникают при более низких значениях D50 , что соответствует содержанию мелких частиц F c более 20%. Чтобы изучить такие расхождения, было бы полезно увидеть, что эмпирическая формула уравнения. ( 9 ) для обычной процедуры состоит из двух терминов.

Второй член Δ R l ( D 50 ) не зависит от значений SPT N ; она зависит исключительно от среднего диаметра частиц D 50 . На рис. 20 значения ΔR l ( D 50 ) также нанесены в зависимости от D 50 . Установлено, что расхождения в оценках Rl из предлагаемой и общепринятой процедур исходят в первую очередь из второго члена Δ R l ( D 50 ). Некоторые из более ранних исследований также предполагали, что сопротивление разжижению ненарушенных образцов илистого песка и ила выше, чем у образцов, восстановленных в лаборатории ( Huang and Huang 2007 ).; и др.), подразумевающих наличие эффектов старения.

Эффекты старения неоднозначны, хотя авторы считают, что присутствие мелких частиц в илистом песке и иле будет способствовать развитию старения в структурах почвенной ткани по сравнению с крупнозернистыми почвами, и что илистый песок и ил будут иметь больший потенциал для развития старения. последствия.

Тем не менее, илистый песок или ил не обязательно будут стареть в структурах почвенной ткани. Следовательно, неясно, действительно ли обычная процедура применима даже к рыхлому илу с более низкими значениями W sw и N sw , которые рассматриваются в настоящем исследовании. В любом случае следует проявлять должную осторожность при применении предлагаемой процедуры к мелкому илу.

На рис. 21 показаны зависимости сопротивления разжижению R l и N’ sw1 , полученные из уравнений (6) , (7) и предложены в настоящем исследовании. Здесь следует отметить, что использование соотношений, показанных на рис. 21 , ограничено удовлетворением, так как ожидается, что эти соотношения будут искривлены внутрь в диапазоне R l от более 0,3 до 0,4. Наличие двух зависимостей R l и N’ sw1 для песка и песка с илом означало бы, что рассматриваемые почвы должны быть классифицированы, по крайней мере, как песок или песок, содержащий ил, хотя в настоящее время тесты SWS не сопровождают ни одну почву. процедуры выборки.

Следовательно, желательно, чтобы геотехнология отбора почвенных проб была разработана с использованием скважин испытаний SWS. В противном случае отсутствие отбора проб почвы в испытаниях SWS можно было бы преодолеть путем получения данных скважины в результате стандартных испытаний на проникновение (SPT), проводимых поблизости.

Распределение критических значений N sw по глубине , разделяющее возможность разжижения грунта на малое или большое, также может быть получено из настоящего исследования, как показано на рис. 22 . Критические значения N sw , полученные в настоящем исследовании, оказались больше, чем обычно найденные в литературе.

4 . Выводы

Предложена эмпирическая методика оценки сопротивления разжижению грунтов R l с помощью шведского весового зондирования. Две эмпирические формулы, уравнения. (6) , (7) , были сначала получены для оценки R l непосредственно из сопротивления проникновению , W sw и N sw , шведских весовых испытаний, а именно, одного для чистого песка, а другого для песка с илом и илистого песка.

Было обнаружено, что предложенная процедура работает хорошо, хотя сравнение предложенной процедуры с традиционной процедурой, основанной на значениях SPT N и D50 , показали, что расхождения возникают при оценке сопротивления разжижению мелкозернистого ила. Поэтому следует проявлять должную осторожность при нанесении его на мелкий ил.